拉格朗日插值
公式
\[L(x) = \sum_{j=0}^{k} y_{j}l_{j}(x)\]其中 \(l_{j}(x) = \prod_{i=0, i \neq j}^{k} \frac{x-x_{i}}{x_{j}-x_{i}}\)
上述公式可以保证 $L(x_{j}) = y_{j}$
给出$n$个点可以确定一个 $n-1$ 次多项式,求出$f(k)$,每求一次k值的时间复杂度为$O(n^2)$代码如下:
1 | |
变形:重心拉格朗日插值法
令 $l(x) = (x-x_{0})(x-x_{1})…(x-x_{k}) = \prod_{i=0}^{k}(x-x_{i})$
则上述 \(l_{j}(x) = \frac{l(x)}{x-x_{j}}\frac{1}{\prod_{i=0, i \neq j}^{k} x_{j}-x_{i}}\) 定义权重$w_{j}$ : \(w_{j} = \frac{1}{\prod_{i=0, i \neq j}^{k} x_{j}-x_{i}}\) $l_{j}(x)$ 可以进一步化为 : \(l_{j}(x) = l(x) \frac{w_{j}}{x-x_{j}}\) 于是有重心拉格朗日多项式 : \(L(x) = l(x) \sum_{j=0}^{k} \frac{w_{j}}{x-x_{j}}y_{j}\) 若此时新增加一个点 $(x_{k+1}, y_{k+1})$
需要更新以下值 :
- $k$ := $ k+1$
- $l(x)$ := $l(x)(x-x_{k+1})$
- $ w_{j} $ := $\frac{w_{j}}{(x_{j}-x_{k+1})}$ 更新所有的$w_{j}$ 需要 $O(n)$ 时间
重心拉格朗日插值(二型)
考虑对函数 $g(x) \equiv 1$ (即 $y_{j} = 1$)进行插值: \(g(x) = l(x) \sum_{j=0}^{k} \frac{w_{j}}{x-x_{j}}\) 则 $L(x) $ 中的$l(x)$ 可以消去,得到重心拉格朗日插值公式二型: \(L(x) = \frac{L(x)}{g(x)} = \frac{\sum_{j=0}^{k} \frac{w_{j}}{x-x_{j}}y_{j}}{\sum_{j=0}^{k} \frac{w_{j}}{x-x_{j}}}\) 此时增加一个点时不必考虑 $l(x)$ 了
例题
自然数k次幂和
给定 $n$ 和 $k$ , 求 $ \sum_{i=1}^{n}i^k $ % mod 的值。(n <= 1e18, k <= 1e6)
当 $k$ 比较小时,例如 $k = 1$ 时有 \(\sum_{i=1}^{n} i = \frac{n(n+1)}{2}\) 易知:$\sum_{i=1}^{n}i^k$ 的最高次幂为 $k+1$ 。所以知道前 $k+2$ 个点$(x_{i}, y_{i})$便可求出 $f(n)$ 的值。
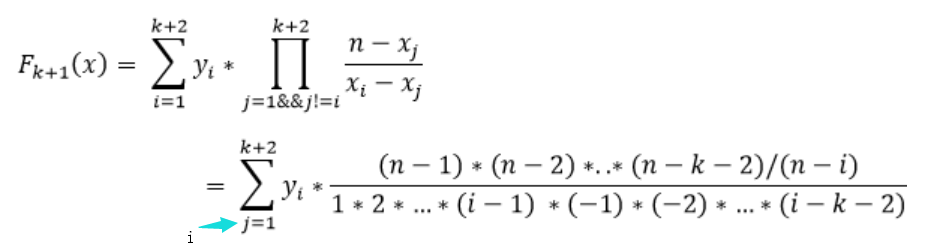
**上式的二式sum中的 j 改为 i **
1 | |
【模板】求多项式系数
1 | |